。例如在一定条件下，可以用等截面杆，取代变截面杆。

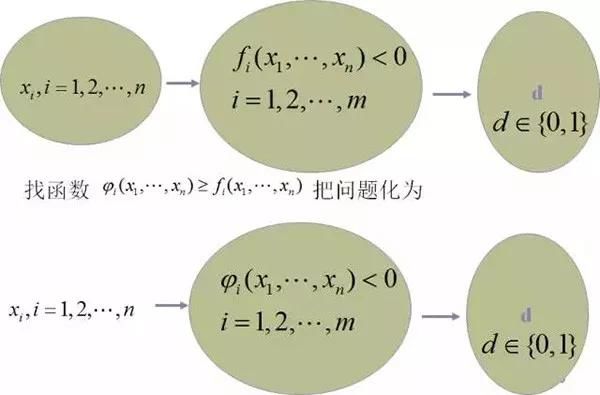
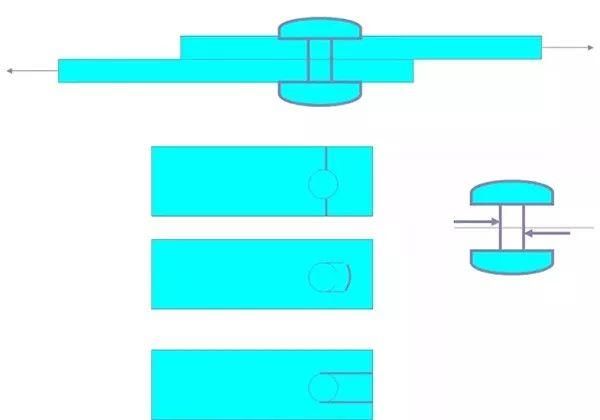
例子

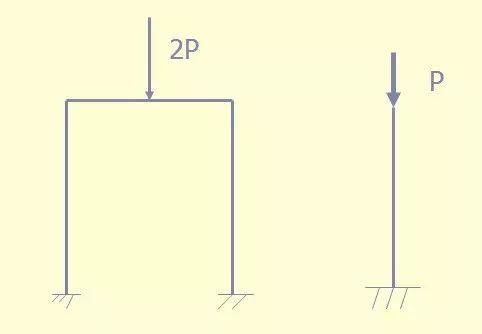
受压框架的稳定性

空心圆环和空心圆球的径向应力在内压相同的条件下，圆球的应力要小。因为前者的变化规律是lnr ，而后者是的变化是1/r。

伦敦阿尔伯特吊桥

Albert Bridge across the River Thames. One of the earliest cable-stayed bridges, it opened in 1873. The spans are 147 ft, 384 ft, and 147 ft. Width of the bridge is a little over 41 ft. (London, England)

阿尔伯特吊桥上便步走公告

1808年，法国皇帝拿破仑率部10万入侵西班牙，当部队以整齐的步伐穿过一座铁索吊桥时，大桥崩塌了。数十年后，在俄国的圣彼得堡，又有一队军人在齐步通过卡坦卡河上的铁桥时，发生了蹋桥事故。

Shreve, Lamb & Harmon: Empire State Building New York, 1931, 1250' ht

Height: 1,472 feet (448 meters) to top of antennae. 1,250 feet (391 meters) to 102nd floor observatory. 1,050 feet (320 meters) to 86th floor observatory.

Rockefeller Center New York, 1930- Height: RCA Building, 850feet (259 meters)70 stores

结论：

• 你应当对有关结构力学的基本定理比较熟悉。例如，应当熟悉有关结构稳定性和极限设计的上下限定理。叠加原理，互易定理等等；
• 你应当比较多地了解结构的各种量的依从关系，即大小变化的定性趋势；
• 你应当尽可能地记忆各种常数和一些典型简单结构解的应力，失稳临界压力和位移等。
• 结构简化和分解是一种非常重要的能力，需要经常练习，以提高这种能力。即使有了计算机，计算时还是要简化，针对实际结构提出计算模型。

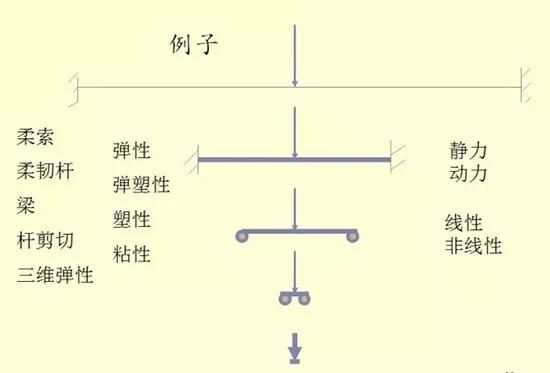
5. 结构模型

结构模型依赖于结构的几何形状，受力特点与大小，所用的材料和所需要求解的问题（强度，稳定性，变形）有比较好的近似。求解比较简单，随计算机的发展简单的含义也在变化。

6. 80%-20%规律

日常事物的粗略统计大都符合80％－20％规律，举例如下：

• 80％的财富集中在20％的人手中，而20％的财富是80％拥有；
• 较高深的80%的知识是20％的人懂得，而较普及的20％的知识是80％的人知道；
• 图书馆借阅次数的80％是20％的书，而其余80％的书出纳次数只有20％；
• 占汉字使用次数80％的只是20％的字，而其余80％的字使用的次数只有20％；
• 盈利80％的产品占产品的20％，而其余80％的产品只盈利20％；
• 任何一件事情，较容易的80％部分常常只需要投入20％工作量，而较难的20％，则需要80％的工作量；
• 你的知识，常用次数的80％是你的知识的20％，而使用次数的20％，要占你的知识80％。

一般事物大都是符合正态分布的统计规律的，即：

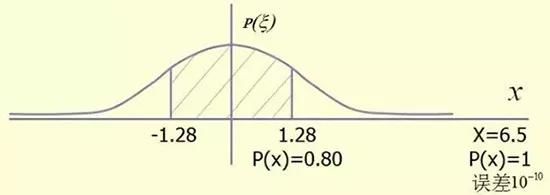
充分地自觉地应用80％－20％规律分析和观察问题，可以使你培养起全局观念。一个好的工程师除了会分析具体的结构而外还要具有全局观点。你如果要成为一个熟练的设计工程师，你的眼光就要注意经常使用的20％的知识。如果你要成为一位富有创新成就的工程师，就还要注目于不经常使用的80％知识。一个好的研究人员和一个好的经营人员所注意的方面是很不同的，社会上出名的人多数只注意不常遇到的80％，而获利最多的人却只注意经常遇到20％。

在做结构分析时我们也应当考虑80％－20％规律。如果将精度（误差）和所付出的努力（例如成本）表为一个函数，这时这个函数也是符合正态分布的。就是说，投入20％可以得到各种精度的80％，如果这种精度已经够用了，就没有必要去努力追求更高的精度。在分析结构时，要求的精度也要适可而止，多余的精度是一种浪费。在结构分析时所用到的各种量以及所求的量，其精度要求应当一致。

文章来源：《力学与实践》 网址: http://www.lxysjzz.cn/zonghexinwen/2021/0707/604.html