发现弹性模量
弹性模量是表征材料弹性变形和结构设计的重要指标。众所周知,1676年,罗伯特·胡克(1635-1703)在1676年给出了弹簧变形与力的关系,即胡克定律,

这里,F表示力,x表示弹簧变形。 k 是表征弹簧弹性变形能力的常数,称为刚度系数(顽固系数)或弹性系数。从式(1)可以看出,k可以通过力计算F与弹簧变形的比值x。弹性模量有点像材料变形中的弹性系数k,但发现它比弹性系数更曲折。

图 1 罗伯特·胡克 (1635 –1703)
这是一张 1680 的肖像。有人推测这大概是胡克
17世纪末,戈特弗里德·威廉·莱布尼茨(Gottfried Wilhelm Leibnitz),1646-1716)微积分的引入很快对欧洲大陆。为了扩大微积分的应用范围,许多科学家提出各种问题来扩大微积分的应用。 Jacob Bernoulli (1654-1705) 提出了一个体现微积分应用的力学问题。他可能是第一个涉及弹性模量的数学家。题目如下:
“如图2(b)所示,在悬臂梁的自由端施加集中载荷P,求梁的挠度曲线。”
图 2 Jacob Bernoulli 和梁的弯曲变形示例
Jacob 的想法是悬臂梁的挠度可以由梁的曲率决定。如果用y表示偏转,存在如下关系:
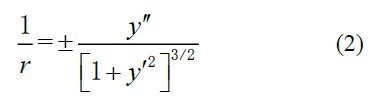
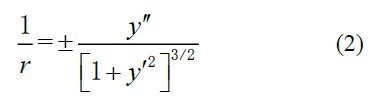 div>
div>上式中,左边的r代表梁弯曲后的曲率半径,代表梁的弯曲程度。显然,梁的弯曲程度与弯矩有关。推到这里后,Jacob 得到如下关系:

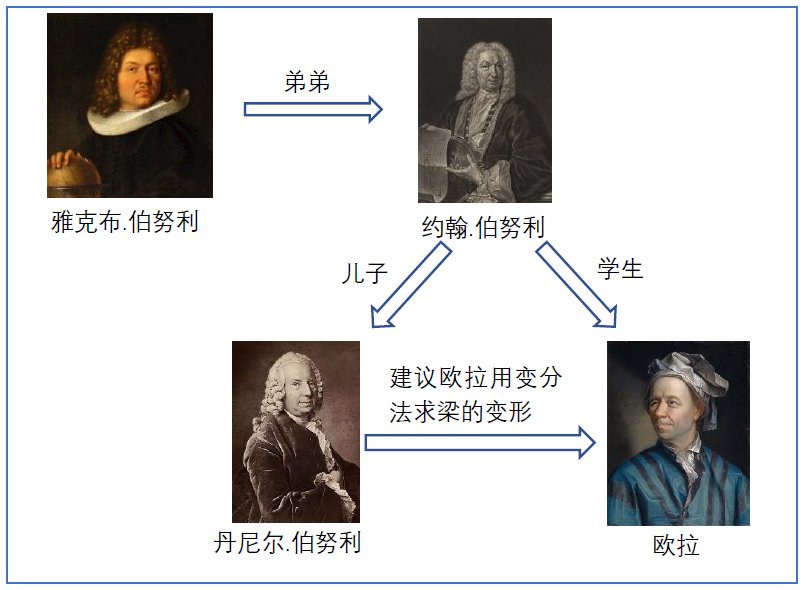
图3从伯努利家族到欧拉
1696年,雅各布的小弟其兄弟约翰·伯努利(Johann Bernoulli,1667-1748)在一封公开信中,向全欧洲的数学家提出了著名的“最陡下降问题”。 ,促成了一种新的学科变体方法的诞生。约翰的儿子丹尼尔·伯努利 (1700-1782) 建议约翰的学生莱昂哈德·欧拉 (1707-1783) 应该使用变分方法来解决雅各布提出的梁变形问题。 Ra 的一封信说:
min,Daniel 提出了 Euler 的问题of 等价于求梁变形时的最小应变能,不考虑常数项,这在力学上称为最小势能原理,该原理认为梁的真实变形必须满足最小应变势能,这是弹性中的最小作用原理。力学中的具体化。
不久之后,欧拉使用变分方法得出了与雅各布斯相同的结果:


在拉动结果中,偏转和长度的平方是错误的,但应该是三次方。另外,系数C是弯曲刚度EI,他把C< /em> 称为“绝对弹性”,认为与材料的弹性特性和梁的横截面形状有关(参考铁木辛哥《材料力学史》)。很多学者提到欧拉在1727年发表的一篇文章提出了弹性模量的概念(缺乏文献),这可能只是对这个概念的一个想法。但即便如此,与雅各布对微积分应用的纯讨论相比,欧拉已经向力学迈进了一步,更重要的是指出了C与材料弹性特性之间的相关性。

从那时起,人们就认为材料的弹性特性也是材料特性之一,并且试图测量各种材料的这种特性。 1782 意大利实验机械师佐丹奴·里卡蒂(Giordano Riccati)利用梁的振动特性确定了钢相对于黄铜的弹性模量。这被认为是确定弹性模量的第一个实验。他得到的结果如下:
但 Giordano Riccati 仍然没有给出弹性模量的概念,但将其视为反映材料弹性特性的参数。 1807 年,Thomas Young (1773-1829) 出版了A Course of Lectures on Natural Philosophy and the Mechanical Arts,明确提出了“弹性模量”(弹性模量)。一个概念,他在文章中写道:

图5 Thomas Young (1773-1829)
'我们可以用同一物质的某一列的重量来表示任何物质的弹性,它可以被命名为它的弹性模量,其中的重量是这样的,它的任何添加都会以相同的比例增加它,因为添加的重量会因它的压力而缩短相同直径的物质的一部分'。
文章来源:《力学与实践》 网址: http://www.lxysjzz.cn/zonghexinwen/2021/0707/603.html