“我们可以使用同一物质某列中的重量代表任何物质的弹性，重量可以用它的弹性模量表示，重量是这样的，当物体被压缩时，物体受到附加压力的缩短量将成正比对重量的增加。"

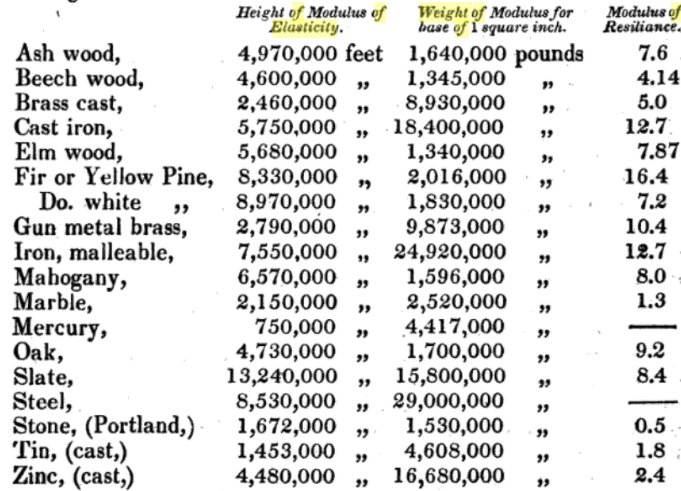
Thomas Young 还指出，这个模量既适用于杆的压缩和伸展，也适用于液体身份证。他还特别强调了胡克定律仅在物体保持弹性变形时才适用，之后发生塑性变形并不再适用。此外，Thomas Young 还测量了多种材料的弹性模量，

不是否认，Thomas Young 对弹性模量的定义比较复杂，他提到的“某一列权重”是不可理解的（我猜他的初衷应该是物质的某种性质）。但他澄清了弹性模量的概念，指出弹性模量是物体的固有特性之一，这与之前工程师利用胡克定律混淆结构刚度和弹性模量的做法有着根本的不同。 .因此，人们也称弹性模量为杨氏模量，以纪念他对物体弹性变形的贡献。

然而，我们今天学习的弹性模量的概念并不是由托马斯·杨给出的，而是由法国机械师克劳德-路易斯·纳维尔（1785-1836）在1826年提出的。在介绍 Navitas 的工作之前，我们需要介绍一下另外两位科学家的工作。

图 6 克劳德-路易斯·纳维尔 (1785-1836)

一个是柯西对应力和应变的定义。 1822年，奥古斯丁·柯西（Augustin Cauchy，1789-1857）在给法国科学院的论文中指出，材料的弹性条件反映了材料的内在性质。这里给出了特性、应力和应变的概念。

图 7 Augustin-Louis Cauchy (1789-1757)

郭士纳使用的单位是“每平方英寸下奥地利磅” ，换算成国际单位制，需要乘以0.0081的系数，最后的结果就是我们现在一般用210GPa。但郭士纳自己将弹性模量称为弹力比。

图 8 Franz Joseph Ritter von Gerstner (1756-1832)< /span>

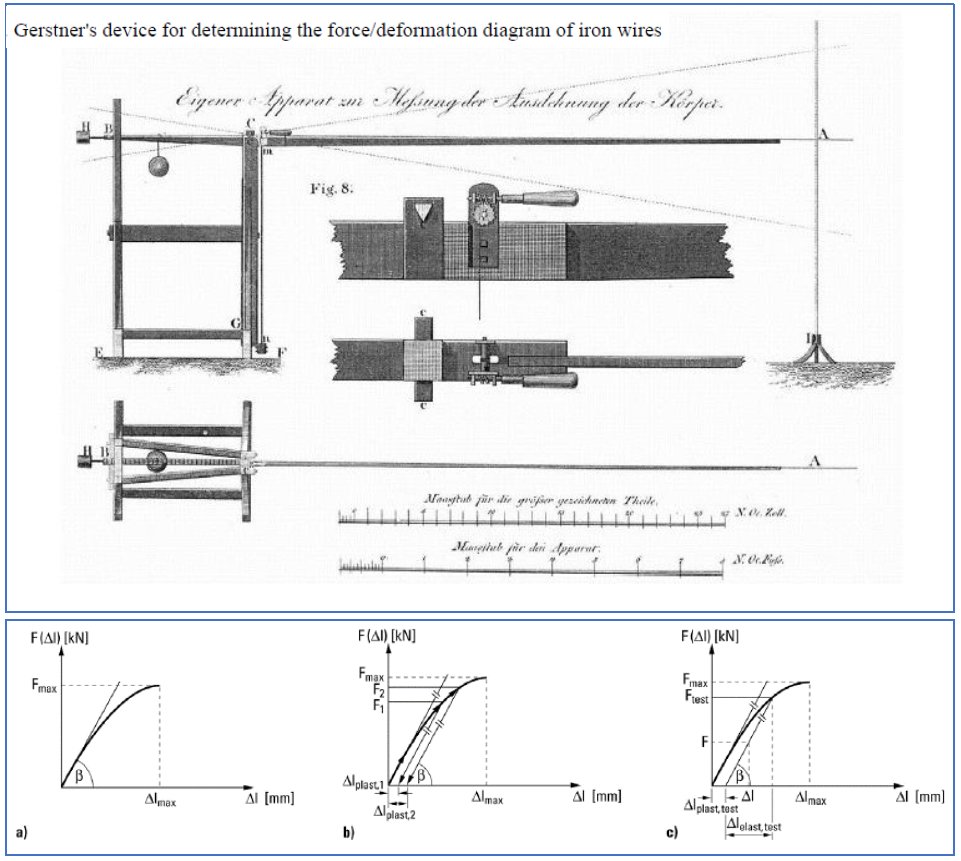
图 9 Gerstner 设计测量力和变形曲线实验装置

有应力应变的概念，有测量材料加载曲线的实验技术。人们很快就会揭开弹性模量的面纱。 1826年，Navitas在分析梁的变形及其强度时，区分了弹性模量（E）和截面惯性矩（I），并给出了矩形截面梁的抗弯刚度如下（注：Navitas是用来表示抗弯刚度的）：

用截面的转动惯量来反映）。在纳维尔的结构理论中，弹性模量占有极其重要的地位，根据弹性模量可以概括材料的力学性能。例如，纳维改变了实验测试计划。经过大量锻铁实验，取平均值作为材料的弹性模型，弹性模量为200 GPa。

弹性模量终于走出阴霾，在力学研究和各种工程建设中发挥了重要作用！

参考文献：

[1] 吴继科。伯努利家族对力学的贡献[J]．力学与实践, 2009(03):105-107.

[2] 常震擑[翻译] Timuxin Ke [工作]“材料力学史”

[3] Chiara Tardini (2015) 评估 19 世纪早期法国木材元素的承载能力，国际期刊建筑遗产，9:5，628-638，

[4] Karl-Eugen Kurrer。论郭士纳《力学手册》中建筑工程与材料强度的关系

[5]百度和维基百科知识

文章来源：《力学与实践》 网址: http://www.lxysjzz.cn/zonghexinwen/2021/0707/603.html